Dragging motion for pile of blocks

This article discusses a scenario/arrangement whose statics/dynamics/kinematics can be understood using the ideas of classical mechanics.
View other mechanics scenarios

The two blocks scenario

Consider one block placed on top of another. The blocks are cuboidal with a horizontal surface of contact. Suppose the lower block is $A$ and the upper block is $B$, and the lower block is resting on a fixed floor. Suppose the coefficients of friction are:

• ${\mu }_{s1}$ is the limiting coefficient of static friction between $A$ and the floor.
• ${\mu }_{k1}$ is the coefficient of kinetic friction between $A$ and the floor.
• ${\mu }_{s2}$ is the limiting coefficient of static friction between $A$ and $B$.
• ${\mu }_{k2}$ is the coefficient of kinetic friction between $A$ and $B$.

We assume that there are no external forces in the vertical direction, other than the gravitational and normal force.

Normal force and gravitational force

On the upper block

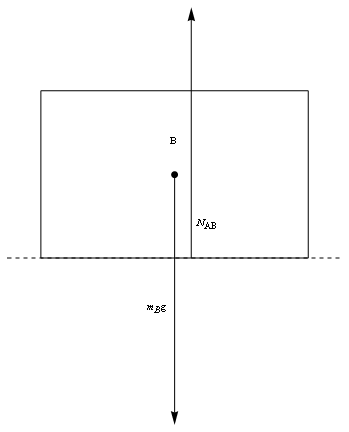
KEY FORCE CONCEPT (ACTION-REACTION): Just because two forces are equal in magnitude and opposite in direction does not imply that they form an action-reaction pair in the sense of Newton's third law of motion. An action-reaction pair is a pair occurs between two bodies that exert forces on each other, not for a pair of forces both acting on the same body. The normal force on the upper block and

$m_{B}g$

(the gravitational force) are equal and opposite but do not form an action reaction pair.

If we denote by $N_{AB}$ the normal force between the blocks, then $N_{AB}$ acts upward on the upper block. The gravitational force $m_{B}g$ acts downward. Since there is no net acceleration in the vertical direction, we get:

$N_{AB}=m_{B}g(1.1)$

On the lower block

If we denote by $N_A$ the normal force between the lower block and the floor, we obtain, by Newton's first law, that:

$N_A=N_{AB}+m_{A}g(1.2)$

Plugging in (1) into (2) we get:

$N_A=(m_A+m_B)g(1.3)$

Intuitively, the weight borne by the floor is the total of the weights of both blocks.

Case of force on lower block

Suppose an external horizontal force $F$ is applied on the lower block. We determine the conditions under which both blocks start moving together, the two blocks start moving but not together, and neither block moves.

Summary of cases

Verbal description of case	Lower bound on $F$ for this case	Upper bound on $F$ for this case	Acceleration of $A$	Acceleration of $B$
Neither block moves	0	$g[{\mu }_{s1}(m_A+m_B)]$	0	0
Both blocks move together with the same acceleration	$g[{\mu }_{s1}(m_A+m_B)]$	$g({\mu }_{s2}+{\mu }_{k1})(m_A+m_B)$	$\frac{F}{m_A+m_B}-{\mu }_{k1}g$	$\frac{F}{m_A+m_B}-{\mu }_{k1}g$
The blocks move with different accelerations	$\frac{F}{m_A+m_B}-{\mu }_{k1}g$	infinite	$\frac{1}{m_A}[F-g({\mu }_{k1}(m_A+m_B)+{\mu }_{k2}{m}_B)]$	${\mu }_{k2}g$

Situation where neither block moves

Denote by $f_{s1}$ the force of static friction between $A$ and the floor, and by $f_{s2}$ the force of static friction between $A$ and $B$.

We get the following equation in the horizontal direction:

$F=f_{s1}+f_{s2}(2.1)$

$f_{s2}\le {\mu }_{s2}{N}_{AB}(2.2)$

On the other hand, the horizontal component of the force diagram of $B$ gives:

$f_{s2}=0(2.3)$

Plugging in (1.3) and (2.2), we get:

$f_{s1}\le {\mu }_{s1}(m_A+m_B)g(2.4)$

Plug (2.3) and (2.4) in (2.1) and obtain:

$F\le {\mu }_{s1}(m_A+m_B)g(2.6)$

Thus, the maximum possible value of external force at which the system does not start accelerating is:

$F_{max}=g[{\mu }_{s1}(m_A+m_B)](2.7)$

{{quotation|ANSWER FORMAT CHECK: For these kinds of situations, the critical values of external forces are always of the form $g$ times a homogeneous linear polynomial involving the masses, with coefficients drawn from various possible friction coefficient.

Situation where blocks move together as a system

Suppose both blocks have an acceleration of $a$ in the direction of the external applied force $F$. Denote by $f_{k1}$ the force of kinetic friction between $A$ and the floor, and by $f_{s2}$ the force of static friction between $A$ and $B$ (the friction is static because the blocks move together so there is no slipping between surfaces). We get:

$F=f_{k1}+f_{s2}+m_{A}a(3.1)$

Also:

$f_{k1}={\mu }_{k1}{N}_A(3.2)$

$f_{s2}\le {\mu }_{s2}{N}_{AB}(3.3)$

and finally, the horizontal force component on $B$ gives:

$f_{s2}=m_{B}a(3.4)$

Plug in (3.2) and (3.4) into (3.1) and get:

$F={\mu }_{k1}{N}_A+m_{B}a+m_{A}a(3.5)$

Plug in (1.3) in here to get:

$F={\mu }_{k1}(m_A+m_B)g+(m_A+m_B)a(3.6)$

Rearranging, we obtain:

$a=\frac{F}{m_A+m_B}-{\mu }_{k1}g(3.7)$

INTUITIVE CHECK: The value of acceleration is the same as what we would get if we assumed a single block of mass

$m_A+m_B$

with coefficient of kinetic friction

${\mu }_{k1}$

with the floor.

Also, we note by plugging in (3.3) into (3.4) that:

$m_{B}a\le {\mu }_{s2}{N}_{AB}(3.8)$

Plugging in (3.7) and (1.1) into (3.8) we get:

$F\frac{m_B}{m_A+m_B}-{\mu }_{k1}{m}_{B}g\le {\mu }_{s2}{m}_{B}g(3.9)$

which rearranges to:

$F\le ({\mu }_{s2}+{\mu }_{k1})(m_A+m_B)g(3.10)$

We already know from (2.7) a lower bound on $F$, so we get, combined, that:

${\mu }_{s1}(m_A+m_B)g\le F\le ({\mu }_{s2}+{\mu }_{k1})(m_A+m_B)g(3.11)$

Situation where blocks move at separate accelerations

Suppose $a_A$ is the acceleration of the lower block and $a_B$ is the acceleration of the upper block. Denote by $f_{k1}$ the force of kinetic friction between $A$ and the floor and by $f_{k2}$ the force of kinetic friction between $B$ and the floor. We get:

$F=f_{k1}+f_{k2}+m_A{a}_A(4.1)$

Also:

$f_{k1}={\mu }_{k1}{N}_A(4.2)$

and

$f_{k2}={\mu }_{k2}{N}_{AB}(4.3)$

The horizontal force component for $B$ gives:

$f_{k2}=m_B{a}_B(4.4)$

Plugging in (4.2) and (4.3) into (4.1), we get:

$F={\mu }_{k1}{N}_A+{\mu }_{k2}{N}_{AB}+m_A{a}_A(4.5)$

Plugging in the values of $N_A$ and $N_B$ from (1.1) and (1.3), we get

$F={\mu }_{k1}(m_A+m_B)g+{\mu }_{k2}{m}_{B}g+m_A{a}_A(4.6)$

This rearranges to

$a_A=\frac{1}{m_A}[F-g({\mu }_{k1}(m_A+m_B)+{\mu }_{k2}{m}_B)](4.7)$

Plugging in (4.3) and (1.1) into (4.4), we get:

${\mu }_{k2}{m}_{B}g=m_B{a}_B(4.8)$

This rearranges to:

$a_B={\mu }_{k2}g(4.9)$

Finally, the constraint on $F$ is that:

$F\ge ({\mu }_{s2}+{\mu }_{k1})(m_A+m_B)g(3.11)$