Applying the Coulomb model of friction
This article discusses how the Coulomb model of friction can be applied to predict values of acceleration and force in given mechanics scenario.
There are three parts to the application:
- Solve assuming static friction.
- Solve assuming kinetic friction.
- Predict which of the cases (static and kinetic friction) arises.
Note that there may be static friction between some pairs of surfaces and kinetic friction between other pairs of surfaces, and we may need to solve for various combinations.
Some general observations:
- If the limiting coefficient of static friction and the coefficient of kinetic friction are equal for all pairs of surfaces in contact, then the Coulomb model of friction can be used to correctly predict all accelerations and the accelerations are continuous (though not differentiable) as functions of various parameters in the scenario (such as angles, external force magnitudes, masses).
- If there is a pair of surfaces for which the coefficient of kinetic friction is strictly smaller than the limiting coefficient of static friction, then there can be a discontinuity at certain values of force or certain angles in the predicted value of acceleration. Further, the predicted values of acceleration are not stable under mild perturbations in these regions of discontinuity.
- The system is generally correctly determined (i.e., neither overdetermined nor underdetermined) to predict values of accelerations once we decide whether static or kinetic friction is operative. However, in the situation of multiple surfaces of contact that are experiencing static friction, it may not be possible using mechanics alone to figure out the magnitudes of static friction operating between multiple surface pairs, even though some sort of total across the surface pairs may be computable.
Assuming static friction
Ignoring rotational issues
We get the following information about the system of equations:
- Equality constraint: The accelerations on both bodies are equal. This follows from the fact that the velocity on both bodies are equal, and when two quantities are identically equal through time, their derivatives are also equal. This can be incorporated either by choosing a single acceleration variable for both bodies, or by choosing different acceleration variables and setting up an equality constraint between them. Note that if one of the bodies is stationary, or moving at constant velocity (so its acceleration is zero) the other body also has acceleration zero.
- Equality constraint: The force of static friction exerted by one body on the other is equal in magnitude and opposite in direction to the force of static friction exerted by the other body on the first.
- Inequality constraint: The magnitude of force of static friction is bounded from above by the limiting coefficient of static friction (denoted ) times the magnitude of normal force. In the limiting case for this, equality occurs.
The role of the inequality constraint is not to help determine the magnitudes of acceleration directly, but rather, to determine necessary constraints on the parameters to the setup for the static friction scenario to apply.
Below are some examples:
| Scenario | Picture | Section in page for static friction analysis |
|---|---|---|
| sliding motion along an inclined plane | 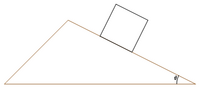 |
Sliding motion along an inclined plane#Component along (down) the inclined plane |
| dragging motion for pile of blocks | 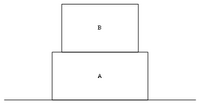 |
Dragging motion for pile of blocks#Situation where neither block moves |
| pulley system on a double inclined plane | 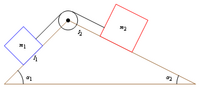 |
Section not yet created, see page anyway. |
Assuming kinetic friction
Ignoring rotational issues
We get the following information about the system of equations:
- Equality constraint: The force of kinetic friction is equal in magnitude to the coefficient of kinetic friction times the magnitude of the normal force, and its direction is opposite the direction of slipping/relative motion along the plane of contact.
Here's how a situation involving kinetic friction is typically solved:
- We first use the component perpendicular to the plane of contact, and Newton's first law in that direction, to obtain the magnitude of the normal force.
- We then plug this value of normal force into the equality constraint to obtain the magnitude of kinetic friction.
- Finally, we plug this into the equation using Newton's first law (case of constant velocity, or equilibrium) or Newton's second law.
Note that if the body being considered is initially at rest and is constrained to move in a straight line, then the direction of acceleration and the direction of velocity should be the same as each other. In particular, if solving the system above gives a direction of acceleration along the direction of the force of kinetic friction, then this means that we made a wrong assumption about the direction of acceleration and velocity, and need to redo the setup.
