Pulley system for block piled on block

The scenario

Consider one block placed on top of another, with the bottom block being $A$ and the block on top being $B$ . $A$ is on a fixed horizontal floor and the surface of contact between $A$ and $B$ is also horizontal. There is a pulley system connecting $A$ and $B$ , with both sides of the pulley rope being horizontal.

Consider the following conventions:

$\mu_{s1}$ is the limiting coefficient of static friction between $A$ and the floor.
$\mu_{k1}$ is the coefficient of kinetic friction between $A$ and the floor.
$\mu_{s2}$ is the limiting coefficient of static friction between $A$ and $B$ .
$\mu_{k2}$ is the coefficient of kinetic friction between $A$ and $B$ .

Assume that $\mu_{k1} \le \mu_{s1}$ and $\mu_{k2} \le \mu_{s2}$ .

We assume the pulley and string to be massless, so that the tension at both ends of the string is equal.

Normal force and gravitational force

On the upper block

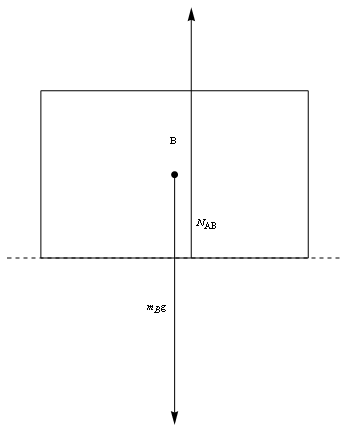
KEY FORCE CONCEPT (ACTION-REACTION): Just because two forces are equal in magnitude and opposite in direction does not imply that they form an action-reaction pair in the sense of Newton's third law of motion. An action-reaction pair is a pair occurs between two bodies that exert forces on each other, not for a pair of forces both acting on the same body. The normal force on the upper block and $m_Bg$ (the gravitational force) are equal and opposite but do not form an action reaction pair.

If we denote by $N_{AB}$ the normal force between the blocks, then $N_{AB}$ acts upward on the upper block. The gravitational force $m_Bg$ acts downward. Since there is no net acceleration in the vertical direction, we get:

$\! N_{AB} = m_Bg \qquad (1.1)$

On the lower block

If we denote by $N_A$ the normal force between the lower block and the floor, we obtain, by Newton's first law, that:

$N_A = N_{AB} + m_Ag \qquad (1.2)$

Plugging in (1) into (2) we get:

$N_A = (m_A + m_B)g \qquad (1.3)$

Case analysis

We consider an external force $F$ applied horizontally, in the direction away from the direction the string is attached, on the lower block. The analysis is exactly the same for the upper block (give explanation). Note the following:

The tension in the string at both its $A$ and $B$ ends is equal.
The accelerations of $A$ and $B$ have equal magnitudes and opposite directions.
In particular, if either block moves, both blocks move and they do so in opposite directions, so there is bound to be slipping. It is not possible for the two blocks to move as a system.

Case that neither block moves

Let $T$ denote the magnitude of tension in the string. There is no slipping of surfaces, so static friction is operative both between $A$ and the floor and between $A$ and $B$ . Denote by $f_{s1}$ the magnitude of static friction between $A$ and the floor and by $f_{s2}$ the magnitude of static friction between $A$ and $B$ .

For block $A$ , we have, by Newton's first law:

$\! F = T + f_{s1} + f_{s2} \qquad (2.1)$

Also:

$f_{s1} \le \mu_{s1}N_A \qquad (2.2)$

and

$f_{s2} \le \mu_{s2}N_{AB} \qquad (2.3)$

For block $B$ , we have, by Newton's first law:

$\! T = f_{s2} \qquad (2.4)$

Plugging in (2.4) into (2.1), we obtain that:

$\! F = f_{s1} + 2f_{s2} \qquad (2.5)$

Plugging in (2.2), (2.3), (1.1), and (1.3) into (2.5), we get:

$\! F \le g[\mu_{s1}(m_A + m_B) + 2\mu_{s2}m_B] = g[\mu_{s1}m_A + (\mu_{s1} + 2\mu_{s2})m_B]$

Case that both blocks move

Let $a$ denote the magnitude of acceleration of both $A$ and $B$ , with the direction for $A$ being along $F$ (pulling on the string) and the direction for $B$ being opposite to $F$ (being pulled by the string). As before, denote by $T$ the tension in the string, which is the same at both ends of the string due to the assumption of a massless string and massless pulley.